Prioritizing Safety Aspects: Advanced Multi-Criteria Decision-Making for Nuclear Power Plant Site Selection in Indonesia

Abdullah, Ade Gafar

Under the patronage of:

Journal Metrics

Impact factor (2022): 2.1

Source Normalized Impact per Paper (SNIP): 0.474

SCImago Journal Rank (SJR): 0.377

Prioritizing Safety Aspects: Advanced Multi-Criteria Decision-Making for Nuclear Power Plant Site Selection in Indonesia

DOWNLOAD FULL TEXT PDF

Original scientific paper

Journal of Sustainable Development of Energy, Water and Environment Systems
Volume 12, Issue 4, December 2024, 1120525
DOI: https://doi.org/10.13044/j.sdewes.d12.0525

Ade Gafar Abdullah

Universitas Pendidikan Indonesia, Bandung, Indonesia

Abstract

Indonesia's energy needs must be met by clean and sustainable energy sources, such as nuclear energy, to achieve the net-zero emission target. A critical issue after the Indonesian government decided to use nuclear energy is the decision-making problem of selecting the most suitable location for a nuclear power plant. This study integrates two methods of multi-criteria decision-making. First, the Fuzzy-Analytical Hierarchy Process and second the Fuzzy-Technique for Order Preference by Similarity to Ideal Solution. Both methods are used to determine the most suitable nuclear power plant location according to safety aspects. The first method is used to determine the priority order of criteria, while the second method is used for ranking alternative locations. Eleven aspects related to safety based on references validated by ten Indonesian nuclear experts through focus group discussion activities are geology, geotechnics, seismology, population density, meteorology, topography, hydrology, cooling water, land use, proximity to hazardous, proximity to wetland, evacuation route, and environment. Meanwhile, the East Kalimantan and West Kalimantan provinces are the two prospective nuclear power plant locations. The analysis results using the first method show that the order of the highest priority criteria for the safety aspect are geology, geotechnics, seismology, population density, and environment. Meanwhile, the second method recommends the West Kalimantan provinces as the most suitable nuclear power plant location, with a preference value of 0.5675. The results of integrating two methods for determining the most suitable site for a nuclear power plant from a safety aspect show that advanced multi-criteria decision-making efficiently and accurately reduces decision bias based on expert opinion.

Keywords: Multi-criteria decision-making; Site selection; NPP; Fuzzy-AHP; Fuzzy-TOPSIS; Safety Aspect; Indonesia.

Views (in 2025): 118 | Downloads (in 2025): 35
Total views: 677 | Total downloads: 187

INTRODUCTION

Given the anticipated surge in Indonesia's energy demands, the energy sector is becoming an essential pillar in achieving the Net-Zero Emissions goal. This increase in demand underscores the importance of developing clean and environmentally friendly energy sources. Furthermore, the sector holds a prominent position as the most significant contributor to carbon emissions. To mitigate the detrimental effects of these emissions, there is a pressing need to transition to clean and sustainable sources, particularly nuclear energy. The decision to adopt nuclear energy introduces the pivotal task of selecting an optimal site for a Nuclear Power Plant (NPP), constituting a critical aspect of the decision-making process [1]. However, this selection process is intricate due to the multifaceted consideration of various factors. These factors include energy conservation and sustainable development, which are integral aspects of effective energy planning [2]. The complexity of site selection for NPP construction necessitates a comprehensive evaluation, incorporating a spectrum of factors, including safety, economic, social, health, ecological, technical, and cost [3]. Improper placement of NPP carries significant risks, underlining the importance of a meticulous assessment of influential factors [4].

Given that coal presently contributes 50% of Indonesia's electricity, followed by gas (29%), renewable energy (14%), and fuel (7%), the use of NPPs is still a viable option for attaining a renewable energy development target of 31% by 2050 [5]. Although approximately 10% of the world's total electricity production is generated by NPP in over 30 countries, a further 15% of extant capacity is in the process of being developed in 50 countries [6].

The impediment of site selection often affects the development of NPP, necessitating a solution for optimal location determination. Furthermore, the decision-making process is influenced by several criteria, and certain key factors can affect the outcome. Multi-Criteria Decision-Making (MCDM) is a strategy for designing and resolving decision-making problems comprising multiple criteria. Several MCDM methods, such as Analytical Hierarchy Process (AHP), Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), ELimination Et Choix Traduisant la Réalité (ELECTRE), Preferences Ranking Organization METHod for Enrichment Evaluations (PROMETHEE), and Grey Theory have been extensively reported in previous studies. TOPSIS was initially developed by Hwang and Yoon [7], with the fundamental principle that the selected alternative must have the shortest distance to the positive ideal solution and the longest distance to the negative ideal solution. In the classic MCDM, the evaluation and weighting of the criteria are defined, but in the classic TOPSIS method, alternative evaluations and weightings of criteria are shown as real values [8]. Fuzzy-AHP and Fuzzy-TOPSIS are among the methods that effectively incorporate qualitative and quantitative analysis. Fuzzy-AHP method is often used to determine the last alternative weight, while Fuzzy-TOPSIS method is typically used to assess alternative rankings [9]. According to a previous study, Fuzzy-TOPSIS method is used to sequence preferences based on similarities with optimal solutions [10]. Meanwhile, Fuzzy-AHP method, with its conventional degree of uncertainty, helps to improve the AHP method, which is the only method for decision-making based on a large number of qualitative and quantitative criteria [11]. Fuzzy-TOPSIS, in particular, offers distinct advantages in handling uncertainty and complexity, making it an effective decision-making tool. This method can also manage scenarios characterized by conflicting decision-making criteria [12].

Fuzzy-AHP and Fuzzy-TOPSIS methods have been widely implemented for various purposes, including computer-integrated manufacturing [13], software needs selection [10], wire electrical discharge machining [14], selecting the best firewall alternative to secure a network [15], implementation of sustainable manufacturing in small and medium-sized enterprises [16], and locating industrial supporting bonded logistics centers [17]. In addition, the combination of the AHP-TOPSIS method has been applied to the risk analysis of hazardous materials transportation in smart cities [18] and to the supply chain, healthcare, business, resource management, engineering, and manufacturing [19]. The AHP method is the most widely used method for determining the location of NPPs [20]. The MCDM method has been used to determine the best and most secure NPP location [1], [3], [21], [22], but there are no recent reports focusing on the safety aspect. Safety is a crucial factor in selecting NPP site, as an inappropriate site choice can harm the adjacent community and environment. An inspection of a highly secure area must be conducted to determine the optimal location for NPP. NPP requires different safety measures than those of heavy industrial facilities and other plants [23]. Therefore, this study addresses three concerns pertinent to this objective:

What are the criteria related to safety aspects to determine the most optimal location of NPPs?

How does the Fuzzy-AHP method determine the priority order of the criteria from the safety aspect, and how does the Fuzzy-TOPSIS method select the best NPPs site?

What are the results of integrating Fuzzy-AHP and Fuzzy-TOPSIS methods to determine the priority order of criteria and the best location for constructing NPPs in East Kalimantan and West Kalimantan provinces?

Integrating Fuzzy-AHP and Fuzzy-TOPSIS methods in selecting suitable NPP sites based on safety aspects is a new approach. It is expected to be a reliable tool for decision-makers. The problem of choosing the best site is a typical MCDM problem with many conflicting attributes. By integrating the two methods, the decision process can be supported in determining the optimal location, and the bias of expert opinions can be reduced. The results of this research are expected to be used as a decision support system in the siting of NPPs in Indonesia.

METHODS

Fuzzy-AHP is a further development of the AHP method for solving complex problems at different hierarchical levels with varying criteria to make the problem more structured and systematic. At each level of the hierarchy, pairwise comparisons are made to determine the importance of the criteria using linguistic terms. Fuzzy-AHP is used when multiple criteria are interrelated and difficult to measure with certainty. This method allows uncertainty to be incorporated into the decision-making process and considers the priority weight of each criterion in the hierarchy created. In the AHP method, the majority of selection parameters were unable to provide precise accuracy due to the inability of the classic AHP to reflect the subjective opinions of humans [24]. Therefore, the Fuzzy assembly concept made the comparison process more flexible and explained the preferences of experts better [25]. Buckley perfected the method by using comparisons based on the trapezium membership function since the linear equation obtained did not always have a unique solution and was dependent on the Fuzzy values of the triangle. Chang introduced a second method of AHP management in 1996 by applying triangle Fuzzy values to the Fuzzy-AHP pair comparison scale and using level analysis to synthesize pair comparison values [26]. At present, several AHP defuzzification methods are still extensively used, including the Chang, Laarhoven, and Buckley methods [27].

A well-known multi-attribute decision maker (MADM) method is TOPSIS, which is often used to solve problems and determine alternatives. The principle of this method was that the chosen alternative should be closest to the positive ideal solution and furthest from the negative ideal solution [28]. The decision maker's rating of each alternative for different criteria and the weight given were first cumulated [29]. Evaluation of various subjective criteria and the weight of the criteria expressed in a linguistic form could be converted into real values. Fuzzy numbers were sets defined by a certain real number interval, and each such interval had membership values between 0 and 1 [30]. The fuzzy triangle number was used to describe the rating of each alternative and the weighting of each criterion. Using a multiplication operation on a triangular Fuzzy number, the multiplication result between the rating and the weight could be calculated as a crisp value. Therefore, without sorting Fuzzy numbers, a fuzzy value could be obtained for positive and negative ideal solution [31].

Study Procedures

The criteria for selecting the NPP site have been developed based on literature reviews. Furthermore, the criteria were then evaluated based on the opinions of experts. The AHP method, whose calculation was performed manually with the assistance of Expert Choice, could be used to determine the criteria's priority order. When the consistent ratio (CR) at the weight of the assessment was ≤ 0.1 or 10%, it could be said to be consistent. In the Fuzzy-AHP and Fuzzy-TOPSIS methods, the values of matrix pairs and priority vectors from the AHP method were used for further calculations to determine location based on criteria.

Characteristics of the Study Area

The provinces of West and East Kalimantan were the study areas for the NPP site. Furthermore, these two provinces met all requirements to be considered for the NPP site location [3].

Data collection

Focus group discussions (FGD) collected data from 8-panel experts with doctorates in science and engineering and more than ten years of work experience at state institutions and the National Research and Innovation Agency. These panels of experts were tasked with establishing criteria for determining location characteristics and policies in line with Indonesian law. Following data collection, the next step was evaluating and analyzing data obtained from the literature review and FGD. The safety-related data most commonly used by experts to determine the siting of NPPs include geology, geotechnics and seismology (GS), population density (PD), environment (EM), cooling water (CW), meteorology (MG), hydrology (HG), proximity to hazardous facilities (PF), topography (TG), land use (LU), proximity to wetlands (PW) and evacuation routes (ER). The data that had been analyzed and evaluated was then classified based on pertinent criteria in selecting alternatives for the NPP construction site. To determine the significance of the selected criteria and alternatives, the hierarchical structure was drawn as depicted in Figure 1, and compare two or more alternatives to the previously established criteria using the pairwise comparison method and the MCDM method.

Figure 1.

The hierarchical structure of NPP site selection

Data Processing

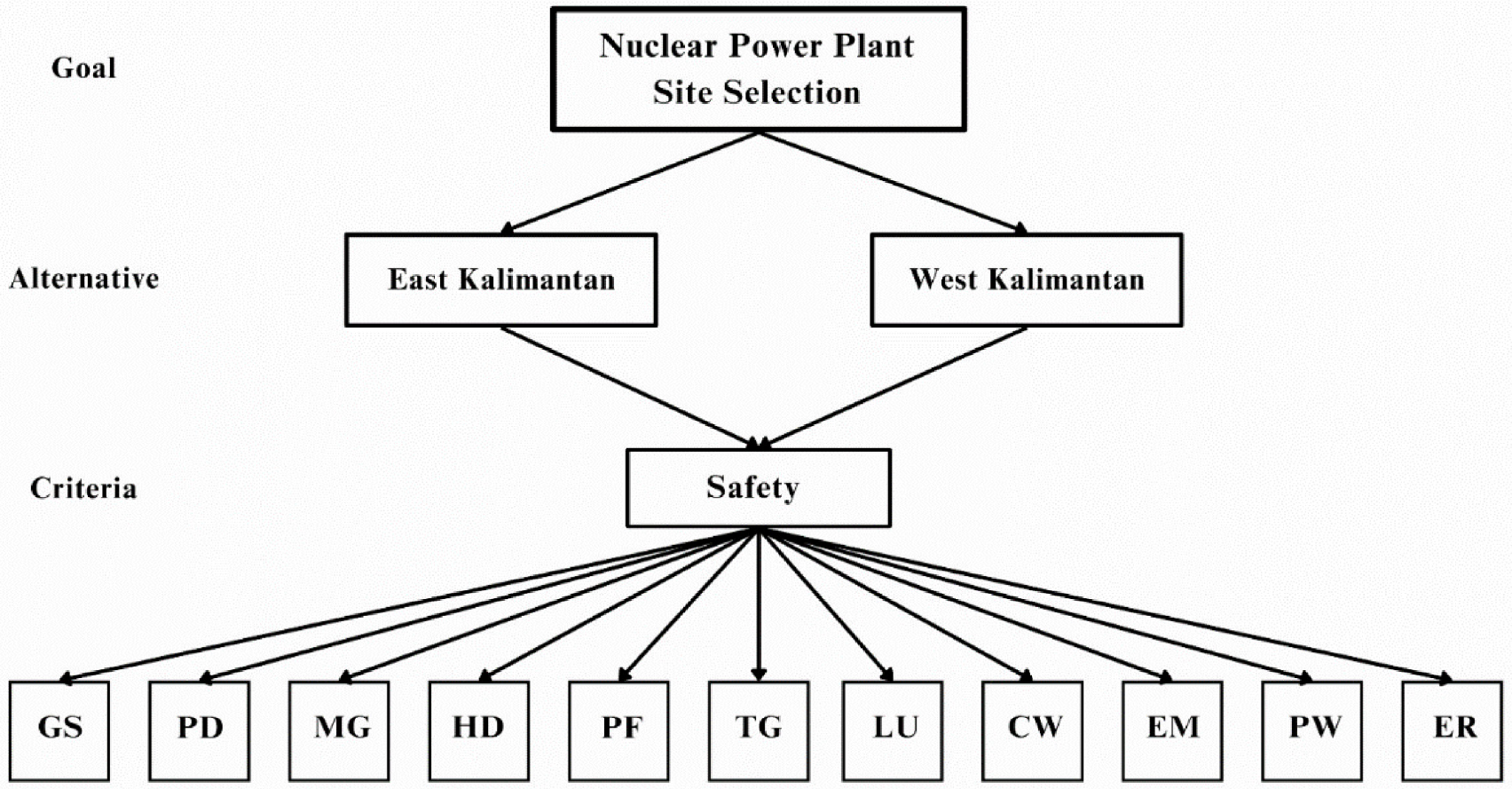
AHP was used to analyze data and determine the relative weight of each criterion using Expert Choice. Furthermore, Fuzzy-AHP and Fuzzy-TOPSIS methods were used to determine the optimal location of NPP. To ensure the veracity of the obtained results, reevaluation was performed when the received values were inconsistent or incoherent.

AHP Stage.

The first action in this AHP stage was to find the criteria from a literature review, ranked based on their importance to identify and determine the most influential criteria in selecting the NPP site. Subsequently, weights were evaluated based on the opinions of experts. The AHP scale of determination referred to [3], and the steps used to complete the AHP stage included:

Compare elements in pairs based on the obtained criteria and create a matrix of comparison pairs with a given weight to show the impact of one element's importance on another.
Normalize the matrix by dividing the value of each paired element by the number of columns in the matrix.
Calculate eigenvalues, the consistency index (CI), and the consistency ratio (CR). A hierarchy was considered consistent when the CR value was less than or equal to 0.1. Furthermore, a recalculation must be performed when CR is less than 0.1.

The random consistency index (RI) value in Table 1 showed the value that could be used in the AHP method, where n was the number of used criteria.

Table 1.

The RI

n	1	2	3	4	5	6	7	8	9	10	11	12
RI	0	0	0.52	0.89	1.12	1.26	1.36	1.41	1.46	1.49	1.52	1.54

Fuzzy-AHP Stage.

In Fuzzy's calculations, a triangular Fuzzy number (TFN) scale with three membership values was used, including low (l), middle (m), and maximum (u). Membership value derived from the TFN transformation was compared to the AHP scale [32]. Fuzzy-AHP calculation procedures included:

Compare pairings using TFN scale values against the AHP scale.
Determining Fuzzy synthesis extent boundary (S_i). To obtain Fuzzy synthesis values, it was necessary to specify the values l, m, and u in the criteria columns derived from the TFN matrix of comparison pairs, [33].

$S_{i} = \sum_{j = 1}^{m} M_{g i}^{j} \times {[\sum_{i = 1}^{n} \sum_{j = 1}^{m} M_{g i}^{j}]}^{- 1}$ (1)

where

$\sum_{j = 1}^{m} M_{g i}^{j} = (\sum_{j = 1}^{m} l_{j}, \sum_{j = 1}^{m} m_{j}, \sum_{j = 1}^{m} u_{j})$ (2)

and

${[\sum_{i = 1}^{n} \sum_{j = 1}^{m} M_{g i}^{j}]}^{- 1} = (\frac{1}{Σ_{j = 1}^{m} l_{j}, Σ_{j = 1}^{m} m_{j}, Σ_{j = 1}^{m} u_{j}})$ (3)

Determining vector priority values. The S_i value was used as a benchmark to determine the vector priority value. When one of the S_i values had a higher degree probability compared to the other, then the vector priority value could be determined after the S_i value had been computed [34]:

$V (M_{2} \geq M_{1}) = \{\begin{matrix} 1 if m_{2} \geq m_{1} \\ 0 if l_{1} \geq u_{2} \\ \frac{l_{1} - u_{2}}{(m_{2} - u_{2}) - (m_{1} - l_{1})} others \end{matrix}$ (4)

where M₁ is the value S_i on criteria 1, and M₂ is the value S_i on criteria 2.

Identify defuzzification values. The minimum value of the vector priority result was used to determine the defuzzification value. For k=1, 2, …n, with k≠i, then obtained

$d' (A_{i}) = min V (S_{i} \geq S_{k})$ (5)

Normalizing weight vector values. This normalization was accomplished by dividing the elements of each column by the number of columns and elements in each row. The results were then summed and divided by the number of elements in each line [35]:

$W' = d' (A_{1}), d' (A_{2}), \dots ., d' {(A_{n})}^{T}$ (6)

where: A_i = 1, 2, …n is the decision element for determining the normalized weight value vectors

$W = \frac{d' (A_{1}), d' (A_{2}), ... ., d' {(A_{n})}^{T}}{W'}$ (7)

Analyzing the factors influencing NPP location decisions using Buckley's Geometric algorithm. In this model, Fuzzy trapezium number was used to evaluate respondents' opinions. After performing the various stages of Fuzzy, the subsequent evaluation matrix was constructed and implemented as follows [36]:

$r_{i} = {(Π_{j = 1}^{m} a_{i j})}^{1 / m}$ (8)

where a_ij is Fuzzy score of the i criteria relative to the j. The geometric mean Fuzzy comparison score for each of the i criteria was:

${\tilde{r}}_{l} = (l_{r i}, m_{r i}, u_{r i}) = [{(Π_{j = 1}^{m} l_{i j})}^{1 / m}, {(Π_{j = 1}^{m} m_{i j})}^{1 / m}, {(Π_{j = 1}^{m} u_{i j})}^{1 / m}]$ (9)

Fuzzy weights for each criterion were then computed using the following formula:

${\tilde{W}}_{l} = {\tilde{r}}_{l} \otimes ({\tilde{r}}_{1} \otimes {\tilde{r}}_{2} \otimes ... . \otimes {\tilde{r}}_{n})$ (10)

The subsequent phase was defuzzification, which comprised transforming the output into a single-value output. After obtaining the crisp value of each criterion, the final weight could be determined by normalizing the crisp value.

Fuzzy-TOPSIS Stage.

Fuzzy-TOPSIS method was based on the concept that the selected alternative considered the shortest distance to a positive ideal solution and the longest distance to a negative ideal solution. The calculation steps in Fuzzy-TOPSIS included:

Conversion of Fuzzy data. Expert-obtained weights were converted to Fuzzy values using Table 2, which provided a linguistic scale for alternatives.

Table 2.

Fuzzy linguistics for an alternative

Linguistics Terms	Triangular (TFN)	Fuzzy	Number
Very Poor (VP)	(1, 1, 3)
Poor (P)	(1, 3, 5)
Medium Good (MG)	(3, 5, 7)
Good (G)	(5, 7, 9)
Very Good (VG)	(7, 9, 9)

Normalization of Fuzzy result matrix using pairwise comparison [37],

${\tilde{r}}_{l j} = (\frac{a_{i j}}{c_{j}^{*}}, \frac{b_{i j}}{c_{j}^{*}}, \frac{c_{i j}}{c_{j}^{*}}) and c_{j}^{*} = \max_{i} \{c_{i j}\} (benefit criteria)$ (11)

${\tilde{r}}_{i j} = (\frac{a_{j}^{-}}{c_{i j}}, \frac{a_{j}^{-}}{b_{i j}}, \frac{a_{j}^{-}}{a_{i j}}) and a_{j}^{-} = \min_{i} \{a_{i j}\} (cost criteria)$ (12)

Normalization of the weighted matrix,

$\tilde{V} = ({\tilde{v}}_{i j}) with {\tilde{v}}_{i j} = {\tilde{r}}_{i j} \times {\tilde{W}}_{i}$ (13)

Determining Fuzzy Positive Ideal Solution (FPIS) and Fuzzy Negative Ideal Solution (FNIS),

$A^{+} = ({\tilde{v}}_{1}^{+}, {\tilde{v}}_{1}^{+}, ... {\tilde{v}}_{n}^{+}) where v_{1}^{+} = max_{i} \{v_{i j}\};$ (14)

$A^{-} = ({\tilde{v}}_{1}^{-}, {\tilde{v}}_{1}^{-}, ... {\tilde{v}}_{n}^{-}) where v_{1}^{-} = min_{i} \{v_{i j}\}$

Determining the distance of each alternative to FPIS and FNIS,

$D_{i}^{+} = \sum_{j = 1}^{n} d ({\tilde{v}}_{i j}, {\tilde{v}}_{j}^{+}); D_{j}^{-} = \sum_{j = 1}^{n} d ({\tilde{v}}_{i j}, {\tilde{v}}_{j}^{-})$ (15)

The following equation was used to derive alternative distance values for each criterion:

$d (\tilde{a}, \tilde{b}) = \sqrt{\frac{1}{3} {(a - a')}^{2} + {(b - b')}^{2} + {(c - c')}^{2}}$ (16)

Determining the value of the closeness coefficient for each alternative.

$C C_{i} = \frac{D_{i}^{-}}{D_{i}^{+} - D_{i}^{-}}$ (17)

Sort alternatives by priority or preference.

RESULTS

Several publications related to "NPP Site," "NPP Location," or "NPP Sitting" were discovered through literature searches conducted on the Scopus and Web of Science (WoS) databases. Furthermore, 27 journals were found to be significantly relevant to the subject of NPP location. As shown in Figure 2, the search yielded 15 criteria, and these aspects were frequently considered by safety experts.

Figure 2.

Safety criteria for NPP site location

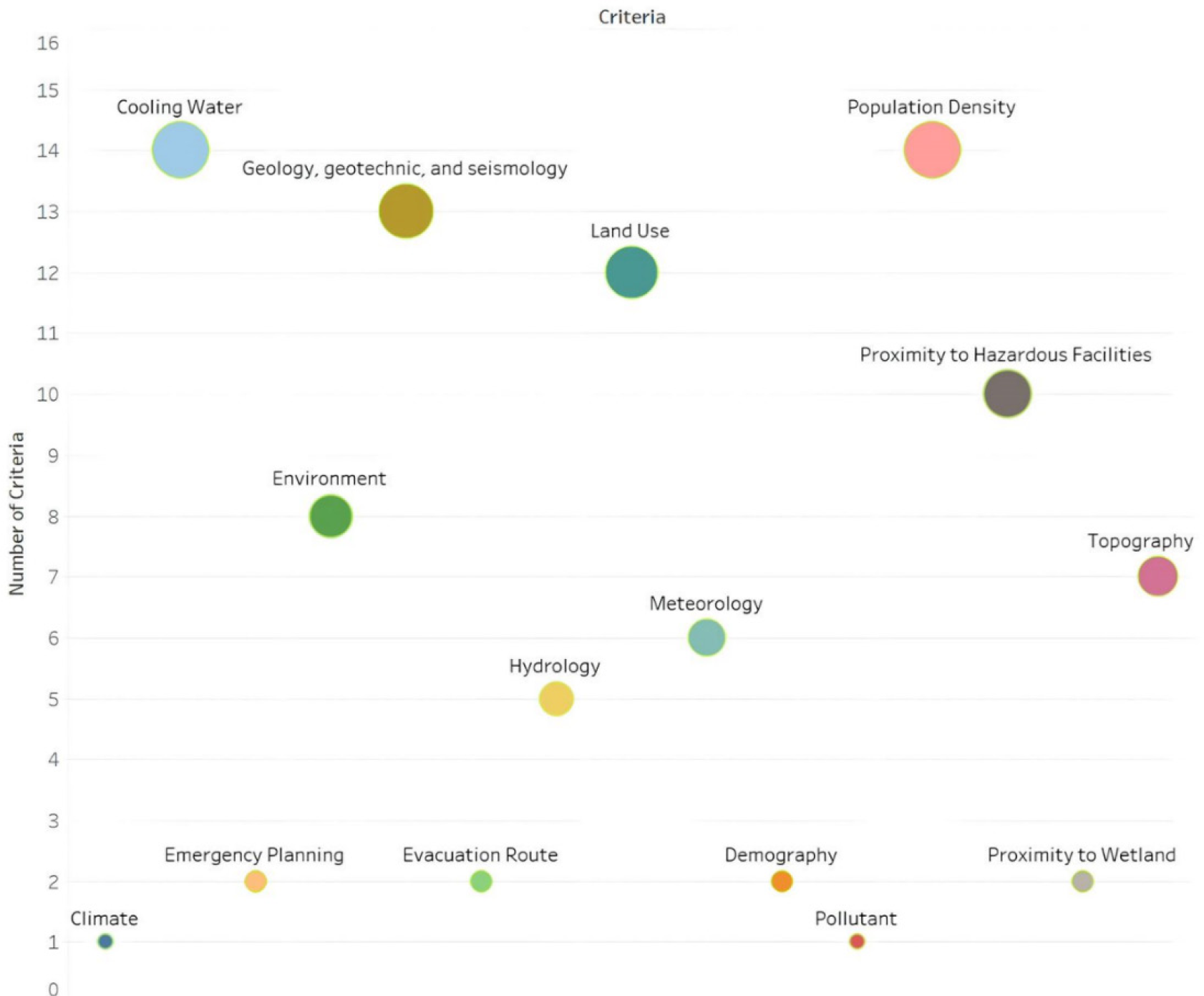
The development of NPP necessitated careful planning of structures, systems, and components to ensure that its operations remained secure under normal and aberrant conditions caused by a variety of internal and external threats [38], [39]. In the FGD, the experts selected 11 criteria from the safety aspect that needed to be considered in determining the location of the NPP site, as shown in Table 3.

Table 3.

Description of safety aspect criteria

Criteria	Description
Geology, Geotechnics and Seismology (GS)	Soil movement and surface stability can be influence geological and seismological conditions. Therefore, it is essential to evaluate external events and potential risks associated with these conditions [40], [41].
Population Density (PD)	A suitable location for the construction of NPPs is away from settlements to avoid the potential damage and danger that can occur around the settlement.
Meteorology (MG)	In determining the location of NPP, meteorological criteria, such as weather, wind, air pollution, temperature, and humidity, must be considered, as well as solar radiation, which can affect safety and interfere with the facility's operations.
Hydrology (HG)	Due to hydrology and oceanography’s interdependence in the in-depth study of location and environment, these two disciplines are combined to identify NPP site with high potential [41].
Proximity to Hazardous (PF)	The potential impact of hazardous facilities from the NPP site location is considered. Geographic information systems collect and analyze information regarding pipelines, roads, railways, airports, and other industrial investments [42].
Topography (TG)	The topography plays a crucial role in determining the location of NPP in terms of the reactor's safety and the construction process. Considerations included soil stability, accessibility, drainage, altitude, and aesthetics.
Land Use (LU)	As NPP location, forests, meadows, and agricultural land are deemed less suitable. The sanctuary area is also not recommended for such purposes [43].
Cooling Water (CW)	It is crucial that sufficient water is available for power plant’s cooling system during normal operation and shutdown.
Environment (ER)	This criterion pertains to the environment, including air, water, soil, climate, vegetation, animals, humans, and their interactions. Thermal pollution caused by the discharge of hot water from the cooling tower into the sea is one of NPP’s most noticeable environment effects.
Proximity to Wetland (PW)	It is crucial to consider proximity to wetlands when selecting site for an NPP, as this can impact on the environment and its ecosystems.
Evacuation Route (ER)	Emergency plans and emergency zones have been created to safeguard NPP facilities, communities, and the environment during emergencies. For emergencies, evacuation routes must be considered.

Criteria Priority

Calculation results using the AHP method.

In creating the hierarchy, the expert panel determined linguistic variables for each pair of criteria by comparing the priorities of the identified criteria. Each linguistic variable is assigned a triangular fuzzy number. A pair-wise comparison matrix is then created using the AHP method to show the influence of the importance of one element on another, as shown in Table 4.

Table 4.

Pairwise comparison matrix between criteria

Criteria	GS	PD	EM	CW	MG	HG	PF	TG	LU	PW	ER
GS	1	3	3	3	5	5	5	7	7	9	9
PD	1/3	1	1	3	3	3	3	5	7	7	9
EM	1/3	1	1	1	3	3	3	5	5	7	9
CW	1/3	1/3	1	1	1	3	3	5	5	7	9
MG	1/5	1/3	1/3	1	1	1	3	3	5	7	7
HG	1/5	1/3	1/3	1/3	1	1	1	3	5	5	7
PF	1/5	1/3	1/3	1/3	1/3	1	1	3	5	5	7
TG	1/7	1/5	1/5	1/5	1/3	1/3	1/3	1	3	5	5
LU	1/7	1/7	1/5	1/5	1/5	1/3	1/5	1/3	1	3	5
PW	1/9	1/7	1/7	1/7	1/7	1/5	1/5	1/5	1/3	1	3
ER	1/9	1/9	1/9	1/9	1/7	1/7	1/7	1/5	1/5	1/3	1
Sum	3.108	6.93	7.654	10.32	15.15	18.00	19.87	32.73	43.53	56.33	71

Table 5.

Normalization of the pairwise comparison matrix

Criteria	Normalization											Sum	Average
GS	0.322	0.433	0.392	0.291	0.330	0.278	0.252	0.214	0.161	0.160	0.127	2.958	0.269
PD	0.107	0.144	0.131	0.291	0.198	0.167	0.151	0.153	0.161	0.124	0.127	1.753	0.159
EM	0.107	0.144	0.131	0.097	0.198	0.167	0.151	0.153	0.115	0.124	0.127	1.513	0.138
CW	0.107	0.048	0.131	0.097	0.066	0.167	0.151	0.153	0.115	0.124	0.127	1.285	0.117
MG	0.064	0.048	0.044	0.097	0.066	0.056	0.151	0.092	0.115	0.124	0.099	0.955	0.087
HG	0.064	0.048	0.044	0.032	0.066	0.056	0.050	0.092	0.115	0.089	0.099	0.754	0.069
PF	0.064	0.048	0.044	0.032	0.022	0.056	0.050	0.092	0.115	0.089	0.099	0.710	0.065
TG	0.046	0.029	0.026	0.019	0.022	0.019	0.017	0.031	0.069	0.089	0.070	0.436	0.040
LU	0.046	0.021	0.026	0.019	0.013	0.019	0.010	0.010	0.023	0.053	0.070	0.311	0.028
PW	0.036	0.021	0.019	0.014	0.009	0.011	0.010	0.006	0.008	0.018	0.042	0.193	0.018
ER	0.036	0.016	0.015	0.011	0.009	0.008	0.007	0.006	0.005	0.006	0.014	0.132	0.012
Sum	1	1	1	1	1	1	1	1	1	1	1	11	1

As shown in Table 5, the next stage was to normalize the matrix between criteria by summing the values on each row of elements and dividing them by the results of the respective criteria rows. Using Table 5 as a reference, the eigenvalue max was computed by multiplying the matrix pairwise comparison with the priority vector, thereby achieving a level of consistency by searching for the CR value, as shown in Table 6.

Table 6.

Eigen value, λ max, RI, CI, CR

Eigenvalue max	λ max - n	RI	CI	CR
12.10	1.10	1.52	0.11	0.07

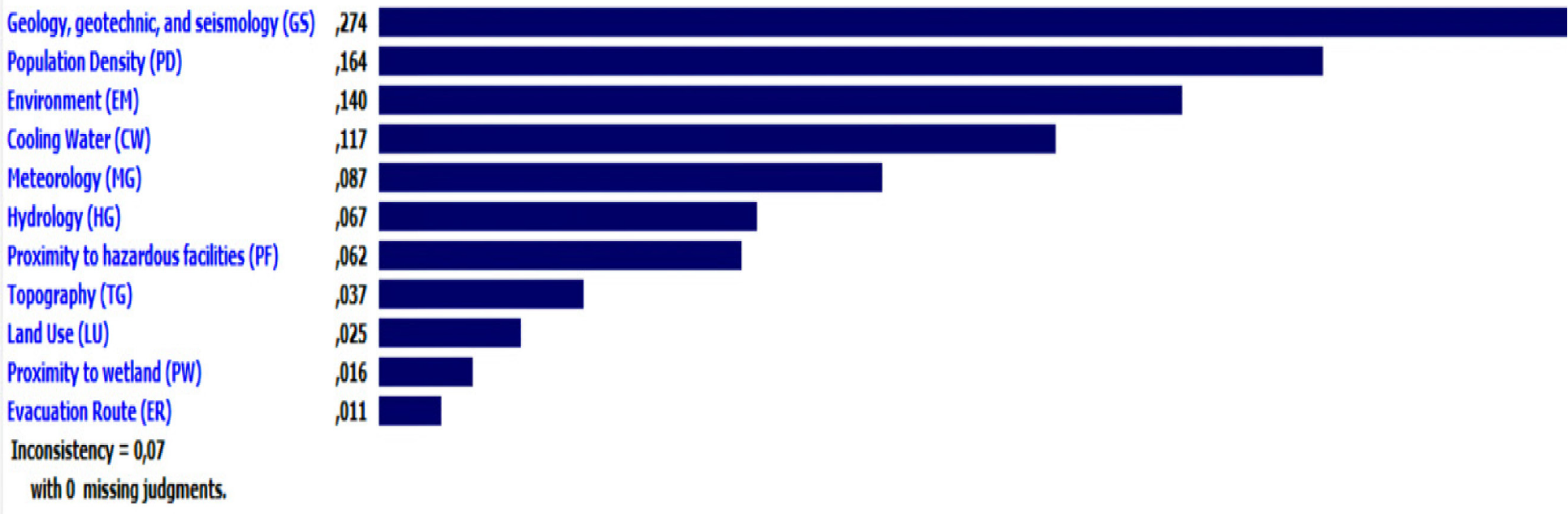
After the calculation was performed using the AHP method, the priority of the criteria was then determined. Priority ranking included GS, PD, EM, CW, MG, HG, PF, TG, LU, PW, and ER. Figure 3 shows the priority order derived from manual AHP calculations using Microsoft Excel and Expert Choice. Furthermore, this calculation yielded a CR of 0.07 and was consistent because its CR was less than 0.1. Based on Figure 3, 11 of the most frequently used criteria were selected for ranking by priority. These specified criteria were assigned consideration weights, and the value of such weights was determined using AHP and Fuzzy-AHP methods.

Figure 3.

Expert Choice assessment result

Calculation results using Fuzzy-AHP method.

Based on Table 7, the pairwise comparison matrix on the obtained weight was converted into a TFN scale, comprising low (l), middle (m), and high (u). The result in Table 7 was used as a reference for calculating the boundary of Fuzzy (S_i) synthesis using the eqs. (1), (2), (3), as shown in Table 8. These synthesis boundaries were then used for the assessment of weight vectors based on the eq., and the results were presented in Table 9.

Table 7.

Conversion of values from the AHP pairwise comparison matrix to the Fuzzy-AHP TFN scale

Criteria	GS			PD				PW			ER
Criteria	l₁	m₁	u₁	l₂	m₂	u₂		l₁₀	m₁₀	u₁₀	l₁₁	m₁₁	u₁₁
GS	1.00	1.00	1.00	2.00	3.00	4.00	…	8.00	9.00	9.00	8.00	9.00	9.00
PD	0.25	0.33	0.50	1.00	1.00	1.00		6.00	7.00	8.00	8.00	9.00	9.00
EM	0.25	0.33	0.50	1.00	1.00	1.00		6.00	7.00	8.00	8.00	9.00	9.00
CW	0.25	0.33	0.50	0.25	0.33	0.50		6.00	7.00	8.00	8.00	9.00	9.00
MG	0.17	0.20	0.25	0.25	0.33	0.50		4.00	5.00	6.00	6.00	7.00	8.00
HG	0.17	0.20	0.25	0.25	0.33	0.50		4.00	5.00	6.00	6.00	7.00	8.00
PF	0.17	0.20	0.25	0.25	0.33	0.50		4.00	5.00	6.00	6.00	7.00	8.00
TG	0.13	0.14	0.17	0.17	0.20	0.25		4.00	5.00	6.00	4.00	5.00	6.00
LU	0.13	0.14	0.17	0.13	0.14	0.17		2.00	3.00	4.00	4.00	5.00	6.00
PW	0.10	0.11	0.13	0.13	0.14	0.17		1.00	1.00	1.00	2.00	3.00	4.00
ER	0.10	0.11	0.13	0.10	0.11	0.13		0.25	0.33	0.50	1.00	1.00	1.00

Table 8.

Fuzzy synthesis boundary (S_i)

Criteria	∑			Fuzzy synthesis boundary (S_i)
Criteria	l	m	u	l	m	u
GS	47.00	57.00	65.00	0.14	0.20	0.28
PD	31.25	38.33	44.50	0.09	0.13	0.19
EM	31.25	38.33	44.50	0.09	0.13	0.19
CW	29.50	35.67	41.00	0.09	0.12	0.18
MG	21.67	26.87	32.25	0.06	0.09	0.14
HG	19.92	24.20	28.75	0.06	0.08	0.12
PF	19.17	23.53	28.25	0.05	0.08	0.12
TG	12.38	15.74	19.42	0.03	0.05	0.08
LU	8.42	10.75	13.33	0.02	0.03	0.05
PW	4.35	5.62	6.96	0.01	0.02	0.03
ER	2.36	2.61	3.00	0.00	0.01	0.01
Sum	227.25	278.65	326.96	0.69	1.00	1.44
Invers	0.0044	0.0035887	0.0030585

Table 9.

Weight vector value

Vector	S1≥	S2≥	S3≥	S4≥	S5≥	S6≥	S7≥	S8≥	S9≥	S10≥	S11≥
S1		0.43734	0.43734	0.32384	0	0	0	0	0	0	0
S2	1		1	0.89863	0.52963	0.3788	0.3510	0	0	0	0
S3	1	1		0.89863	0.9764	0.3788	0.3510	0	0	0	0
S4	1	1	1		0.6207	0.8770	0.4390	0	0	0	0
S5	1	1	1	1		0.8629	0.8291	0.3244	0	0	0
S6	1	1	1	1	1		0.9636	0.4469	0	0	0
S7	1	1	1	1	1	1		0.4896	0	0	0
S8	1	1	1	1	1	1	1		0.5376	0	0
S9	1	1	1	1	1	1	1	1		0.2092	0
S10	1	1	1	1	1	1	1	1	1		0
S11	1	1	1	1	1	1	1	1	1	1
Minimal	1	0.4373	0.4373	0.3238	0	0	0	0	0	0	0
Normal	0.4548	0.1989	0.1989	0.1473	0	0	0	0	0	0	0

The processing of Fuzzy's data was performed using Buckley's Geometric Mean method in eq. (8), and the weight of Fuzzy was calculated with eq. (9). Furthermore, the crisp value was determined and normalized to ensure that Fuzzy-AHP weights were obtained based on Table 10 to determine the criteria's priority order.

Table 10.

Buckley's geometric mean

Criteria	Fuzzy Geometric Mean			Fuzzy Weight			Crisp	Normal
Criteria	l	m	u	l	m	u
SA1	3.5639	4.4447	5.1766	0.1853	0.2753	0.3933	0.2846	0.2715444
SA2	1.9482	2.3844	2.7997	0.1013	0.1477	0.2127	0.1539	0.1468216
SA3	1.9482	2.3844	2.7997	0.1013	0.1477	0.2127	0.1539	0.1468216
SA4	1.6127	1.9527	2.3175	0.0838	0.1210	0.1761	0.1270	0.1211
SA5	1.1343	1.3815	1.6732	0.0590	0.0856	0.1271	0.0906	0.0863934
SA6	0.9389	1.1314	1.3851	0.0488	0.0701	0.1052	0.0747	0.0712739
SA7	0.8278	1.0239	1.3005	0.0430	0.0634	0.0988	0.0684	0.0652745
SA8	0.4768	0.5928	0.7572	0.0248	0.0367	0.0575	0.0397	0.0378536
SA9	0.3354	0.4096	0.5133	0.0174	0.0318	0.0390	0.0294	0.0280567
SA10	0.2194	0.2602	0.3035	0.0114	0.0188	0.0231	0.0178	0.0169376
SA11	0.1563	0.1787	0.2102	0.0081	0.0008	0.0160	0.0083	0.0079022
Sum	13.162	16.144	19.237				1.0482	1
Normal	0.0760	0.0619	0.0520

The priority order of the criteria was determined based on the crisp values presented in Table 10. The greater the crisp value, the greater the chances that the criteria were likely to become a priority. Fuzzy-AHP method yielded the precedence order of criteria, namely GS, PD, EM, CW, MG, HG, PF, TG, LU, PW, and ER.

Fuzzy-TOPSIS calculation.

After obtaining the criteria weight to determine the order of priority using Fuzzy-AHP method, the result was used as an alternative assessment weight in Fuzzy-TOPSIS method. As shown in Table 11, the weight of the criteria was divided into two categories, including benefits and costs. When the value of a criterion was higher, it was placed in the advantage category, and when the value was lower, it was placed in the disadvantage category.

Table 11.

Category of criteria Fuzzy-TOPSIS

	GS	PD	EM	CW	MG	HG	PF	TG	LU	PW	ER
Value	0.2689	0.1594	0.1376	0.1168	0.0868	0.0685	0.0645	0.0397	0.0282	0.0176	0.012
Category	benefit	cost	benefit	cost	cost	cost	benefit	cost	benefit	benefit	cost

After designating the category for each criterion, the weight value of each criterion obtained from expert judgment against each alternative was converted into the TFN scale, as shown in Table 12. Furthermore, the TFN scale was used to characterize uncertainty in assessment based on linguistic terms.

Table 12.

TFN linguistic scale

Criteria	East Kalimantan			West Kalimantan
	l	m	u	l	m	u
GS	1	1	3	3	5	7
PD	3	5	7	1	1	3
EM	1	3	5	1	1	3
CW	1	1	3	3	5	7
MG	1	1	3	1	1	3
HG	1	3	5	1	1	3
PF	1	1	3	1	3	5
TG	1	1	3	3	5	7
LU	1	1	3	1	3	5
PW	1	1	3	1	1	3
ER	1	1	3	1	1	3

The resulting matrix was normalized using eqs. (11) and (12), and the weighted matrix was normalized using eq. (13). The scales were obtained from Table 13. This method comprised weighing each Fuzzy-AHP criterion, thereby assigning a weight to each element of the weighted matrix. As shown in Table 13, the second calculation of these normalizations yielded positive and negative ideal solutions for each criterion.

Table 13.

Positive and negative ideal values

Criteria	East Kalimantan			West Kalimantan			A+	A-
Criteria	l	m	u	l	m	u	A+	A-
GS	0.03841	0.03841	0.11524	0.11524	0.19207	0.26890	0.269	0.038
PD	0.02277	0.03188	0.05313	0.05313	0.15940	0.15940	0.159	0.023
EM	0.01966	0.01966	0.05897	0.05897	0.09829	0.13760	0.138	0.020
CW	0.03893	0.11680	0.11680	0.01669	0.02336	0.03893	0.117	0.017
MG	0.02893	0.08680	0.08680	0.02893	0.08680	0.08680	0.087	0.029
HG	0.02283	0.02283	0.06850	0.02283	0.06850	0.06850	0.069	0.023
PF	0.01290	0.01290	0.03870	0.01290	0.03870	0.06450	0.065	0.013
TG	0.01323	0.03970	0.03970	0.00567	0.00794	0.01323	0.040	0.006
LU	0.00564	0.00564	0.01692	0.00564	0.01692	0.02820	0.028	0.006
PW	0.00587	0.00587	0.01760	0.00587	0.00587	0.01760	0.018	0.006
ER	0.00400	0.01200	0.01200	0.00400	0.01200	0.01200	0.012	0.004

With the values of the positive and negative ideal solutions in Table 13, it was possible to calculate an alternative distance to the fuzzy positive ideal solutions (FPIS) and fuzzy negative ideal solutions (FNIS) using eq. (14). The FPIS value is obtained from the maximum value of the upper (u) scale on the criteria against the alternative, while the FNIS value is obtained from the minimum value of the lower (l) scale. The results were then inserted into eq. (17) to determine the alternative rank based on the criteria shown in Table 14.

Table 14.

Alternative distance to FPIS and FNIS

Alternative	D+	D-	CC_i	Normal	Rank
East Kalimantan	0.88843	1.07248	0.54693	0.49076	2
West Kalimantan	0.68645	0.90082	0.56753	0.50924	1

From the alternative distance to FPIS and FNIS, an ideal alternative rating to the established criteria was determined. West Kalimantan ranked first with a score of 0.5675, and East Kalimantan ranked second with a rating of 0.5469. This explained that as the CC_i value increased the possibility of alternatives being selected also increased.

DISCUSSION

This study devised a decision-making instrument using two MCDM methods, Fuzzy-AHP and Fuzzy-TOPSIS, to determine the location of NPPs based on various criteria supporting safety aspect. Several assessment criteria must be prioritized to choose the most important. Furthermore, two integrated methods, namely the AHP and Fuzzy-AHP both used in risk assessment of options, required a weighing of the criteria [44]. The Fuzzy-AHP method was capable of reflecting ambiguous opinions by transforming them into Fuzzy value. This showed that by conducting calculations using Fuzzy-AHP equation, the priority order of criteria based on the safety aspect could be determined. The results showed that nuclear reactor deployment safety was the primary factor in determining the best site for NPP construction [45]. The three primary criteria for the Fuzzy-AHP analysis results included GS.

Criteria Priority Order

In this study, GS was the order of priority for the first criterion. NPP must be positioned at a secure distance from seismic activity [46] to avoid zones with potentially fluid-containing soil layers, soft soils, abnormalities, elevated plains with high water content, and surface basal cavities [47]. Several studies have also shown that soil and geological stability was an essential factor [26]. Based on geotechnical and geophysical experiments, site characteristics had a significant impact on earthquake evaluation [48]. An ideal site for NPP deployment [49] was located in a zone with a possibility of deformation of the surface soil and a radius of 8 km from the possible earthquake and its surrounding fractures.

The second criterion as a priority was PD, where locations with low levels were ideal for NPP to minimize impact and increase safety. Areas with very dense populations could increase radiological risks, specifically when there is a release of radioactivity into the environment [40]. Therefore, the permissible location for NPP must be approximately 8 km away from populated areas [50]. The PD surrounding NPP development area must also be less than 193 persons per km² [45].

The results showed that environment (EM) was the third priority criterion in this study. When environmental criteria were not considered during the planning and construction phases, it could lead to radioactive waste pollution, lowered groundwater levels, diminished water quality, an increased risk of flooding, and anomalous habitat changes [49]. The marine vegetation could also be affected when the condenser coolant leaked heated water into the ocean, negatively impacting aquatic life. The limit temperature difference between the water released by NPP and seawater was 1°C or less [51]. Furthermore, there were conservation areas, such as national parks and nature reserves to consider. According to previous studies, the permitted distance between NPP and a conservation area was 16 km [49].

Determination of Nuclear Power Plant Site in Indonesia

To determine the most suitable site for NPP, alternative site had to be evaluated while considering safety concerns. The evaluation was carried out to identify a site that satisfied the relevant criteria and met the requirements for NPP development. Each location alternative was analyzed in depth in this evaluation process to determine its suitability and potential to support NPP development.

Based on environmental factors, Kalimantan's continental foundation was responsible for the island's stable position on the Eurasian plate [39]. East Kalimantan, known for its significant PD, was home to several large cities, such as Balikpapan and Samarinda, which attracted many inhabitants due to their industrial and economic opportunities. Several studies have shown that this activity provided a significant contribution to PD. Meanwhile, West Kalimantan had a lower PD compared to East Kalimantan, with a population of approximately 5.26 million and an area of 146.807 km² [52]. The province also had a large but less densely populated territory, and several important cities, such as Pontianak, serving as hubs of economic activity and trade.

Both East and West Kalimantan had river systems that influenced their hydrological conditions. High rainfall during the rainy season increases river drainage. It could lead to flooding, which was a crucial factor in determining the potential use of hydroelectric energy to support NPP operations. Rivers, such as the Mahakam and Kapuas were the region's primary water sources, while lakes and reservoirs served as additional sources.

NPP operations had a significant impact on the environment due to their widespread effect on a variety of habitats and animals. The East Kalimantan region was often used for environmental purposes to a lesser extent than the West Kalimantan region, which could disrupt the local ecosystem and habitat. Furthermore, there were numerous wetland areas in West Kalimantan, including Lake Sentarum National Park, which is renowned for its biodiversity and designated as a Ramsar site. The Kapuas River, the longest river in Indonesia, traveled through this region and sustained wet ecosystems. The area also contained wetlands like the Mahakam River Delta and surrounding barley forests. The vastness of East and West Kalimantan made it possible to access the ER between the two territories. Several studies have shown that the orientation of the wind was a factor to consider in this regard.

The primary criteria in determining the alternative location of the Fuzzy-TOPSIS method was the weighing of the obtained criteria against the alternatives that had considered. Since the priority order of the criteria was the determining factor for the location of NPP, the AHP criteria weight was used to conduct calculations on the Fuzzy-TOPSIS method. However, before Fuzzy-TOPSIS could be applied, the specified criteria must be classified as either cost or advantage criteria (benefit). After obtaining the weight and category of the criteria, the alternative location sequence acquired with the results of West Kalimantan was a more suitable site for an NPP than East Kalimantan. This was because West Kalimantan better fulfilled the ideal NPP construction site criteria. The region was still dependent on energy imports from Sarawak, Malaysia, for 30% or 200 MW of its energy requirements [53]. Furthermore, there was a weakness in the national energy system due to the incapacity to manage power sources that used domestic energy sources. Previous reports showed a reserve of 45,730 tons of uranium suitable for use in power facilities in West Kalimantan, providing additional support for establishing of the West Kalimantan NPP.

CONCLUSION

This study integrates the Fuzzy-AHP and Fuzzy-TOPSIS methods to identify 11 criteria from safety aspects most frequently used by experts in determining the location of NPPs. These criteria include geology, geotechnics and seismology (GS), population density (PD), environment (EM), cooling water (CW), meteorology (MG), hydrology (HG), proximity to hazardous facilities (PF), topography (TG), land use (LU), proximity to wetlands (PW) and evacuation route (ER).
Based on calculations using the Fuzzy AHP method, it was found that geology, geotechnics, seismology (GS), population density (PD), and environment (EM) had the highest priority among the 11 criteria considered. This calculation was carried out using Microsoft Excel and Expert Choice software. The results of this calculation give a Consistency Ratio (CR) value of 0.07 or 7%. As the CR value is less than the standard limit of 10% applied in the AHP method, it can be concluded that the calculation is consistent.
The fuzzy TOPSIS method was applied to select two alternative proposed sites for the NPP, namely in East Kalimantan and West Kalimantan provinces, based on 11 criteria determined from the safety aspect. The calculated results show that West Kalimantan was selected as a potential site for NPP operations with a preference value of 0.5675. Meanwhile, East Kalimantan received a preference value of 0.5469, making it the second choice.
Future research could strengthen the results of this study by identifying and using new MCDM algorithms. The opinions of the people of West Kalimantan regarding the location of the NPP should also be taken into account.

ACKNOWLEDGMENT

This research was funded by Universitas Andalas in accordance with the research contract: Indonesian Collaborative Research (RKI) Scheme B (Co-Host) Number: 7/UN16.19/PT.01.03/ Energi-RKI+ Skema B (Mitra)/2023.

REFERENCES

Erdoʇan M., Kaya I., A combined fuzzy approach to determine the best region for a nuclear power plant in Turkey, Appl. Soft Comput. J., Vol. 39 , pp 84–93, 2016, https://doi.org/https://doi.org/10.1016/j.asoc.2015.11.013
Kaya İ., Çolak M., Terzi F., A comprehensive review of fuzzy multi criteria decision making methodologies for energy policy making, Energy Strateg. Rev., Vol. 24 , pp 207–228, 2019, https://doi.org/https://doi.org/10.1016/j.esr.2019.03.003
Abdullah A., Shafii M., Pramuditya S., Setiadipura T., Anzhar K., Multi-criteria decision making for nuclear power plant selection using fuzzy AHP: Evidence from Indonesia, Energy AI, Vol. 14 , 2023, https://doi.org/https://doi.org/10.1016/j.egyai.2023.100263
Rizzo P., Melissa Dubinsky, Erdem Onur Tastan, Sandra C., MianoSite Selection for Nuclear Power Plants., 2015, https://www.scopus.com/inward/record.uri?eid=2-s2.0-0015975197&partnerID=40&md5=b5fe8bad46bffcbc7e1df842667aedac
Council S., Indonesia Energy Outlook (IEO) 2019, 2019
Salsabila K., Saraswati R., Shidiq I., Susiati H., GIS-based multi-criteria analysis for nuclear power plant site selection in West Kalimantan, IOP Conf. Ser. Earth Environ. Sci., Vol. 623 (1), 2021, https://doi.org/https://doi.org/10.1088/1755-1315/623/1/012049
Dymova L., Sevastjanov P., Tikhonenko A., An approach to generalization of fuzzy TOPSIS method, Inf. Sci. (Ny)., Vol. 238 , pp 149–162, 2013, https://doi.org/https://doi.org/10.1016/j.ins.2013.02.049
Torfi F., Farahani R., Rezapour S., Fuzzy AHP to determine the relative weights of evaluation criteria and Fuzzy TOPSIS to rank the alternatives, Appl. Soft Comput. J., Vol. 10 (2), pp 520–528, 2010, https://doi.org/https://doi.org/10.1016/j.asoc.2009.08.021
Kurt Ü., The fuzzy TOPSIS and generalized Choquet fuzzy integral algorithm for nuclear power plant site selection - A case study from Turkey, J. Nucl. Sci. Technol., Vol. 51 (10), pp 1241–1255, 2014, https://doi.org/https://doi.org/10.1080/00223131.2014.918524
Nazim M., Wali Mohammad C., Sadiq M., A comparison between fuzzy AHP and fuzzy TOPSIS methods to software requirements selection, Alexandria Eng. J., Vol. 61 (12), pp 10851–10870, 2022, https://doi.org/https://doi.org/10.1016/j.aej.2022.04.005
Solangi Y., Longsheng C., Shah S., Assessing and overcoming the renewable energy barriers for sustainable development in Pakistan: An integrated AHP and fuzzy TOPSIS approach, Renew. Energy, Vol. 173 , pp 209–222, 2021, https://doi.org/https://doi.org/10.1016/j.renene.2021.03.141
Rajak M., Shaw K., Evaluation and selection of mobile health (mHealth) applications using AHP and fuzzy TOPSIS, Technol. Soc., Vol. 59 , 2019, https://doi.org/https://doi.org/10.1016/j.techsoc.2019.101186
Zare Banadkouki M., Lotfi M., Selection of computer-integrated manufacturing technologies using a combined fuzzy analytic hierarchy process and fuzzy TOPSIS, Int. J. Ind. Eng. Prod. Res., Vol. 32 (1), pp 105–120, 2021, https://doi.org/https://doi.org/10.22068/ijiepr.32.1.105
Fuse K., Integration of fuzzy AHP and fuzzy TOPSIS methods for wire electric discharge machining of titanium (Ti6Al4V) alloy using RSM, Materials (Basel)., Vol. 14 (23), 2021, https://doi.org/https://doi.org/10.3390/ma14237408
Cubukcu C., Cantekin C., Using a combined fuzzy-AHP and topsis decision model for selecting the best firewall alternative, J. Fuzzy Ext. Appl., Vol. 3 (3), pp 192–200, 2022
Abdullah A., Saraswat S., Talib F., Barriers and strategies for sustainable manufacturing implementation in SMEs: A hybrid fuzzy AHP-TOPSIS framework, Sustain. Manuf. Serv. Econ., Vol. 2 , pp 100012, 2023, https://doi.org/https://doi.org/10.1016/j.smse.2023.100012
Syafrianita, Putro H., Yudoko G., Fahmi F., A combined fuzzy AHP with fuzzy TOPSIS to locate industrial supporting bonded logistics centers, Telkomnika (Telecommunication Comput. Electron. Control., Vol. 21 (4), pp 797–804, 2023, https://doi.org/https://doi.org/10.12928/TELKOMNIKA.v21i4.23973
Kanj H., Kotb Y., Alakkoumi M., Kanj S., Dynamic Decision Making Process for Dangerous Good Transportation Using a Combination of TOPSIS and AHP Methods with Fuzzy Sets, IEEE Access, Vol. 12 , pp 40450–40479, 2024, https://doi.org/https://doi.org/10.1109/ACCESS.2024.3372852
Chaube S., An Overview of Multi-Criteria Decision Analysis and the Applications of AHP and TOPSIS Methods, Int. J. Math. Eng. Manag. Sci., Vol. 9 (3), pp 581–615, 2024, https://doi.org/https://doi.org/10.33889/IJMEMS.2024.9.3.030
Susiati H., Widiawaty M., Dede M., Sunardi, Ryanto T., Handono K., Criteria and methods in nuclear power plants siting: a systematic literature review, Cogent Soc. Sci., Vol. 10 (1), 2024, https://doi.org/https://doi.org/10.1080/23311886.2024.2354976
Akar A., Uyan M., Yalpir S., Spatial evaluation of the nuclear power plant installation based on energy demand for sustainable energy policy, Vol. 26 (4), 2024, https://doi.org/https://doi.org/10.1007/s10668-023-03061-y
Mahmudah R., Putri D., Abdullah A., Shafii M., Hakim D., Setiadipura T., Developing a Multi-Criteria Decision-Making model for nuclear power plant location selection using Fuzzy Analytic Hierarchy Process and Fuzzy VIKOR methods focused on socio-economic factors, Clean. Eng. Technol., Vol. 19 , pp 100737, 2024, https://doi.org/https://doi.org/10.1016/j.clet.2024.100737
Fadeenko V., Remote environmental monitoring in the area of a nuclear power plant, IOP Conf. Ser. Earth Environ. Sci., Vol. 390 (1), 2019, https://doi.org/https://doi.org/10.1088/1755-1315/390/1/012022
Seçme N., Bayrakdaroǧlu A., Kahraman C., Fuzzy performance evaluation in Turkish Banking Sector using Analytic Hierarchy Process and TOPSIS, Expert Syst. Appl., Vol. 36 (9), pp 11699–11709, 2009, https://doi.org/https://doi.org/10.1016/j.eswa.2009.03.013
Kahraman C., Cebeci U., Ulukan Z., Multi‐criteria supplier selection using fuzzy AHP, Logist. Inf. Manag., Vol. 16 (6), pp 382–394, 2003, https://doi.org/https://doi.org/10.1108/09576050310503367
Ekmekçioğlu M., Kutlu A., Kahraman C., A Fuzzy Multi-Criteria SWOT Analysis: An Application to Nuclear Power Plant Site Selection, Int. J. Comput. Intell. Syst., Vol. 4 (4), pp 583, 2011, https://doi.org/https://doi.org/10.2991/ijcis.2011.4.4.15
Ahmed F., Kilic K., Fuzzy Analytic Hierarchy Process: A performance analysis of various algorithms, Fuzzy Sets Syst., Vol. 362 , pp 110–128, 2019, https://doi.org/https://doi.org/10.1016/j.fss.2018.08.009
Mahdavi, Mahdavi-Amiri N., Heidarzade A., Nourifar R., Designing a model of fuzzy TOPSIS in multiple criteria decision making, Appl. Math. Comput., Vol. 206 (2), pp 607–617, 2008, https://doi.org/https://doi.org/10.1016/j.amc.2008.05.047
Chu T., Facility location selection using fuzzy topsis under group decisions, Int. J. Uncertainty, Fuzziness Knowldege-Based Syst., Vol. 10 (6), pp 687–701, 2002, https://doi.org/https://doi.org/10.1142/S0218488502001739
Ashtiani B., Haghighirad F., Makui A., ali Montazer G., Extension of fuzzy TOPSIS method based on interval-valued fuzzy sets, Appl. Soft Comput. J., Vol. 9 (2), pp 457–461, 2009, https://doi.org/https://doi.org/10.1016/j.asoc.2008.05.005
Yong D., Plant location selection based on fuzzy TOPSIS, Int. J. Adv. Manuf. Technol., Vol. 28 (7–8), pp 839–844, 2006, https://doi.org/https://doi.org/10.1007/s00170-004-2436-5
Chang D., Applications of the extent analysis method on fuzzy AHP, Eur. J. Oper. Res., Vol. 95 (3), pp 649–655, 1996, https://doi.org/https://doi.org/10.1016/0377-2217(95)00300-2
Kengpol A., Rontlaong P., Tuominen M., A Decision Support System for Selection of Solar Power Plant Locations by Applying Fuzzy AHP and TOPSIS: An Empirical Study, J. Softw. Eng. Appl., Vol. 06 (09), pp 470–481, 2013, https://doi.org/https://doi.org/10.4236/jsea.2013.69057
KaurSehra S., Singh Brar Y., Kaur N., Multi Criteria Decision Making Approach for Selecting Effort Estimation Model, Int. J. Comput. Appl., Vol. 39 (1), pp 10–17, 2012, https://doi.org/https://doi.org/10.5120/4783-6989
Perçin S., Use of fuzzy AHP for evaluating the benefits of information-sharing decisions in a supply chain, J. Enterp. Inf. Manag., Vol. 21 (3), pp 263–284, 2008, https://doi.org/https://doi.org/10.1108/17410390810866637
Firoozi M., Goodarzi M., Shirali R., Assessment and Potential Survey of Lands in Khuzestan Province Using the Buckley Geometric Mean Model and Geographic Information System (GIS), Open J. Geol., Vol. 07 (03), pp 234–241, 2017, https://doi.org/https://doi.org/10.4236/ojg.2017.73016
NǍdǍban S., Dzitac S., Dzitac I., Fuzzy TOPSIS: A General View, Procedia Comput. Sci., Vol. 91 , pp 823–831, 2016, https://doi.org/https://doi.org/10.1016/j.procs.2016.07.088
Almalki R., Piwowar J., Siemer J., Geographical considerations in site selection for small modular reactors in saskatchewan, Geosci., Vol. 9 (9), pp 1–20, 2019, https://doi.org/https://doi.org/10.3390/geosciences9090402
Susiati H., Udiyani P., Setiawan M., An external event identification for Nuclear Power Plant (NPP) siting project at West Kalimantan, Indonesia, IOP Conf. Ser. Earth Environ. Sci., Vol. 986 (1), 2022, https://doi.org/https://doi.org/10.1088/1755-1315/986/1/012066
Basri N., Ramli A., Selection of Possible Candidate Area for Nuclear Power Plant In Johor, Malaysia, J. Nucl. Relat. Technol., Vol. 9 (1), pp 56–63, 2012
Site Evaluation for Nuclear Installations, 2019, http://www-ns.iaea.org/standards
Baskurt Z., Aydin C., Nuclear power plant site selection by Weighted Linear Combination in GIS environment, Edirne, Turkey, Prog. Nucl. Energy, Vol. 104 , pp 85–101, 2018, https://doi.org/https://doi.org/10.1016/j.pnucene.2017.09.004
, Site Survey and Site Selection for Nuclear Installations, 2015
Shin D., Shin Y., Kim G., Comparison of Risk Assessment for a Nuclear Power Plant Construction Project Based on Analytic Hierarchy Process and Fuzzy Analytic Hierarchy Process, J. Build. Constr. Plan. Res., Vol. 04 (03), pp 157–171, 2016, https://doi.org/https://doi.org/10.4236/jbcpr.2016.43010
Agyekum E., Amjad F., Aslam F., Ali A., Application of Weighted Linear Combination approach in a Geographical Information System environment for nuclear power plant site selection: the case of Ghana, Ann. Nucl. Energy, Vol. 162 , pp 108491, 20072021, https://doi.org/https://doi.org/10.1016/j.anucene.2021.108491
Susiati H., Dede M., Widiawaty M., Ismail A., Udiyani P., Site suitability-based spatial-weighted multicriteria analysis for nuclear power plants in Indonesia, Heliyon, Vol. 8 (3), pp e09088, 2022, https://doi.org/https://doi.org/10.1016/j.heliyon.2022.e09088
Abudeif A., Abdel Moneim A., Farrag A., Multicriteria decision analysis based on analytic hierarchy process in GIS environment for siting nuclear power plant in Egypt, Ann. Nucl. Energy, Vol. 75 , pp 682–692, 20192015, https://doi.org/https://doi.org/10.1016/j.anucene.2014.09.024
James N., Sitharam T., Padmanabhan G., Pillai C., Seismic microzonation of a nuclear power plant site with detailed geotechnical, geophysical and site effect studies, Nat. Hazards, Vol. 71 (1), pp 419–462, 2014, https://doi.org/https://doi.org/10.1007/s11069-013-0919-0
Barzehkar M., Dinan N., Salemi A., Environmental capability evaluation for nuclear power plant site selection: a case study of Sahar Khiz Region in Gilan Province, Iran, Environ. Earth Sci., Vol. 75 (12), 2016, https://doi.org/https://doi.org/10.1007/s12665-016-5825-9
Idris R., Abd. Latif Z., GIS multi-criteria for power plant site selection, Proc. - 2012 IEEE Control Syst. Grad. Res. Colloquium, ICSGRC 2012, 2012
Ahangari R., Noori-Kalkhoran O., A study of the protective actions for a hypothetical accident of the Bushehr nuclear power plant at different meteorological conditions, Radiat. Environ. Biophys., Vol. 58 (2), pp 277–285, 2019, https://doi.org/https://doi.org/10.1007/s00411-018-00775-w
, Provinsi Kalimantan Barat Dalam Angka 2023, 2023
Santosa S., Khotimah K., Andani I., Kumaraningrum A., Nuclear energy development self-management concept to support national energy security and national defense (case study: Commercial NPP plans in the West Kalimantan region), IOP Conf. Ser. Earth Environ. Sci., Vol. 753 (1), 2021, https://doi.org/https://doi.org/10.1088/1755-1315/753/1/012050

Criteria	East Kalimantan			West Kalimantan
	l	m	u	l	m	u
GS	1	1	3	3	5	7
PD	3	5	7	1	1	3
EM	1	3	5	1	1	3
CW	1	1	3	3	5	7
MG	1	1	3	1	1	3
HG	1	3	5	1	1	3
PF	1	1	3	1	3	5
TG	1	1	3	3	5	7
LU	1	1	3	1	3	5
PW	1	1	3	1	1	3
ER	1	1	3	1	1	3

Criteria	East Kalimantan			West Kalimantan
	l	m	u	l	m	u
GS	1	1	3	3	5	7
PD	3	5	7	1	1	3
EM	1	3	5	1	1	3
CW	1	1	3	3	5	7
MG	1	1	3	1	1	3
HG	1	3	5	1	1	3
PF	1	1	3	1	3	5
TG	1	1	3	3	5	7
LU	1	1	3	1	3	5
PW	1	1	3	1	1	3
ER	1	1	3	1	1	3

Criteria	East Kalimantan			West Kalimantan
	l	m	u	l	m	u
GS	1	1	3	3	5	7
PD	3	5	7	1	1	3
EM	1	3	5	1	1	3
CW	1	1	3	3	5	7
MG	1	1	3	1	1	3
HG	1	3	5	1	1	3
PF	1	1	3	1	3	5
TG	1	1	3	3	5	7
LU	1	1	3	1	3	5
PW	1	1	3	1	1	3
ER	1	1	3	1	1	3